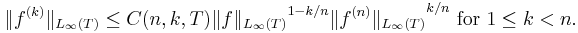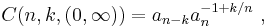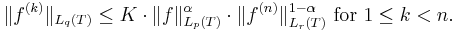Landau–Kolmogorov inequality

In mathematics, the Landau–Kolmogorov inequality, named after Edmund Landau and Andrey Kolmogorov, is the following family of inequalities between different derivatives of a function f defined on a subset T of the real numbers[1]:

\|f^{(k)}\|_{L_\infty(T)} \le C(n, k, T) {\|f\|_{L_\infty(T)}}^{1-k/n} {\|f^{(n)}\|_{L_\infty(T)}}^{k/n} \text{ for } 1\le k < n.

Contents

On the real line

For k = 1, n = 2, T=R the inequality was first proved by Edmund Landau[2] with the sharp constant C(2, 1, R) = 2. For arbitrary n, k, the inequality was proved by Isaac Jacob Schoenberg,[3] the sharp constants are however still unknown.

On the half-line

Following earlier contributions by Jacques Hadamard and Georgiy Shilov, Andrey Kolmogorov found the sharp constants for T=(0, ∞) and arbitrary n, k[4]:

C(n, k, (0, \infty)) = a_{n-k} a_n^{-1%2Bk/n}~,

where an are the Favard constants.

Generalisations

There are many generalisations, which are of the form

\|f^{(k)}\|_{L_q(T)} \le K \cdot {\|f\|^\alpha_{L_p(T)}} \cdot {\|f^{(n)}\|^{1-\alpha}_{L_r(T)}}\text{ for }1\le k < n.

Here all three norms can be different from each other (from L1 to L∞, with p=q=r=∞ in the classical case) and T may be the real axis, semiaxis or a closed segment.

Notes

  1. ^ Weisstein, E.W.. "Landau-Kolmogorov Constants". MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Landau-KolmogorovConstants.html. 
  2. ^ Landau, E. (1913). "Ungleichungen für zweimal differenzierbare Funktionen". Proc. London Math. Soc. 13: 43–49. 
  3. ^ Schoenbergfirst=I.J. (1973). "The Elementary Case of Landau's Problem of Inequalities Between Derivatives.". Amer. Math. Monthly 80: 121–158. 
  4. ^ Kolmogorov, A. (1962). "On Inequalities Between the Upper Bounds of the Successive Derivatives of an Arbitrary Function on an Infinite Integral". Amer. Math. Soc. Translations. 1–2: 233–243.